TIL3 - 2023.09.22

👨‍💻 TIL

TIL3 - 2023.09.22

zunwon 2023. 9. 23. 12:55

자료구조 & 알고리즘

자료구조 + 알고리즘 = 프로그램

자료구조

메모리를 효율적으로 사용하며 데이터를 빠르고 안정적으로 처리하는 것이 궁극적인 목표로 상황에 따라 유용하게 사용될 수 있도록 특정 구조를 이루고 있다
상황에 따라 올바른 자료구조를 선택하는 능력이 필요하다
일차원인 컴퓨터 메모리를 현실에 대응되도록 구조를 만든 것이라 할 수 있음

알고리즘

특정 문제를 메모리 효율적이고 빠른 성능으로 해결하는 것이 궁극적인 목표로 정해진 일련의 절차나 방법을 공식화한 형태로 표현한 것을 말한다.

자료구조와 알고리즘이 중요한 이유

기초 코딩 능력을 기르기 위해 => 자료구조와 알고리즘을 공부하면 능력 UP

문제 해결 능력

논리적 사고 : 어떠한 현상이 존재할 때 추론하고 구조화하여 해답을 내는 것
전산화 능력 : 현실에 있는것을 컴퓨터세계 즉 소프트웨어로 구현하는 것, 논리를 조합하여 컴퓨터 사고가 가능한지
엣지 케이스 탐색 : 예외 상황을 얼마나 잘 찾는지

자료구조의 종류

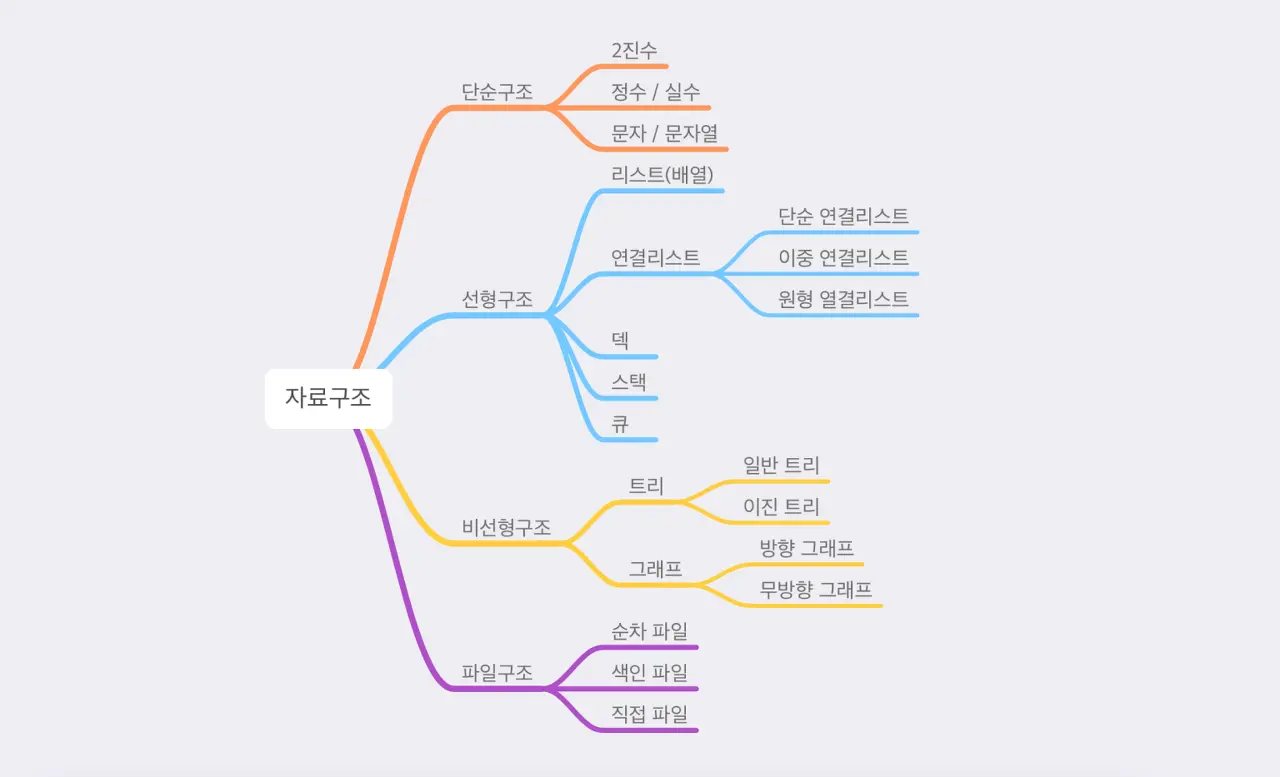
단순 구조

정수, 실수, 문자열, 논리

선형 구조

한 원소 뒤에 하나의 원소 만이 존재하는 형태로 자료들이 선형으로 나열되어 있는 구조
배열, 연결 리스트, 스택, 큐

비선형 구조

원소 간 다대다 관계를 가지는 구조로 계층적인 구조나 망형 구조를 표현하기에 적절
컴퓨터의 폴더 구조, 인간 관계를 나타내기 적합함
트리, 그래프

완벽한 자료구조는 없다 !!! 우리는 상황에 맞게 적절한 자료구조를 선택하자

시간 복잡도

시간 복잡도

프로그램의 성능을 알기 위해 고려 할것
입력 크기, 하드웨어 성능, 운영체제 성능, 컴파일러 최적화, 비동기 로직
따라서 프로그램의 성능을 정확히 파악하는 것을 불가능에 가깝다

빅오 표기법(Big-O notation)

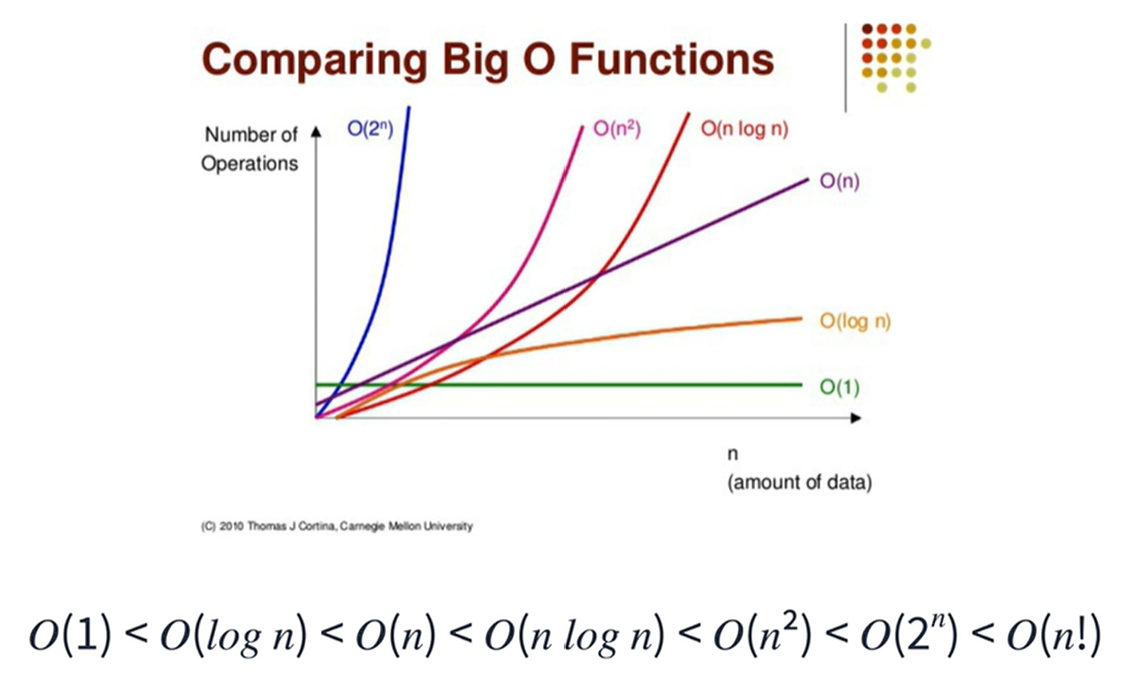
빅오 표기법은 접근적 표기법을 따른다
접근적 표기법 : 함수의 증감 추세를 비교하는 방법

빅오 표기법의 4가지 법칙

계수 법칙 : n이 무한에 가까울 수록 k의 크기는 의미가 없기 때문에 빅오 표기법에서는 생략하여 표기한다

// 두 루프는 같은 O(n)으로 표기된다.
for(let i = 0; i < n; i += 1){
    // ....
}

for(let i = 0; i < n * 5; i += 1){
    // ....
}

합의 법칙 : 빅오끼리는 더해질 수 있다

// 두 루프를 합쳐 O(n + m)으로 표기할 수 있다.
// 계수 법칙에 의해 5는 사라진다
for(let i = 0; i < n; i += 1){
    // ....
}

for(let i = 0; i < m * 5; i += 1){
    // ....
}

곱의 법칙 : 빅오끼리는 곱해질 수 있다

// 두 루프를 합쳐 O(n*2)으로 표기할 수 있다.
// 계수 법칙에 의해 5는 사라진다
for(let i = 0; i < n; i += 1){
    for(let j = 0; j < n * 5; j += 1){
        // ....
    }
}

다항 법칙 : 다항식일 때 표기하는 법

// 다음 루프는 O(n^3)으로 표기할 수 있다.
for(let i = 0; i < n * n * n; i += 1){
    // ....
}

2가지만 기억하기

상수항은 무시

가장 큰 항 외엔 무시

성능 측정 방법

Date 객체를 이용

const start = new Date().getTime();
// ...
const end = new Date().getTime();
console.log(end - start);

배열, 순차 리스트(Array)

배열

연관된 데이터를 연속적인 형태로 구성된 구조
배열에 포함된 원소는 순서대로 번호(index)가 붙는다

배열의 특징

고정된 크기를 가지며 일반적으로 동적으로 크기를 늘릴 수 없지만 자바스크립트처럼 대부분의 스크립트 언어는 동적으로 크기가 증감된다
원하는 원소의 index를 알고 있다면 O(1)로 원소를 찾을 수 있다
원소를 삭제하면 해당 index는 당겨지지 않고 빈자리가 된다

배열 요소 삭제 / 추가

삭제 후 순서를 맞추려면 O(n)이 소요된다

중간에 요소를 추가하고 싶다면 O(n)이 소요된다

따라서 추가와 삭제가 반복되는 로직이라면 배열 사용을 권장하지 않는다!

연결리스트(Linked List)

추가와 삭제가 반복되는 로직이라면 어떻게 해야할까??

연결 리스트

각 요소를 포인터로 연결하여 관리하는 선형 자료구조
각 요소는 노드라고 부르며 데이터 영역과 포인터 영역으로 구성된다

연결 리스트의 특징

메모리가 허용하는 한 요소를 제한없이 동적으로 추가할 수 있다
탐색에 O(n)이 소요
요소를 추가하거나 제거할 때는 O(1)이 소요
Singly Linked List, Doubly Linked List, Circular Linked List가 존재

배열과 연결 리스트의 차이

배열 : 순차적인 데이터가 들어가서 메모리의 영역을 연속적으로 사용
연결리스트 : 순차적이지 않기 때문에 각 데이터가 퍼져 있어 포인터를 사용하여 각 영역을 참조

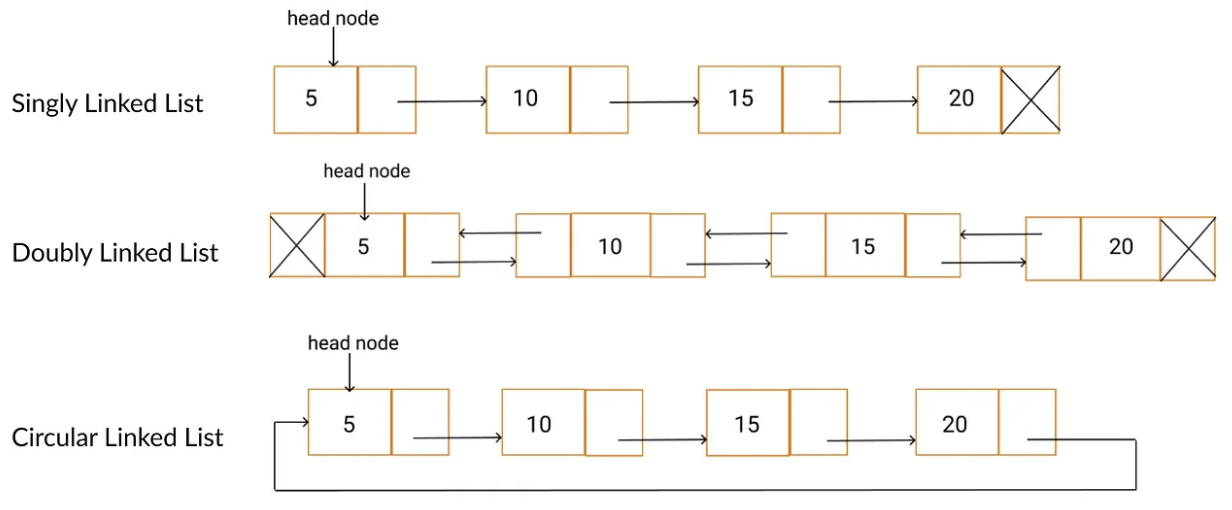
Singly Linked List (단일 연결 리스트)

Head → Tail까지 단방향으로 이어지는 연결 리스트
remove시 자동으로 가비지컬렉터에 의해서 사라진다

데이터 찾기

Head 포인터를 참고하여 Head를 찾고 맞는지 확인 후 다르면 다음 요소로 넘어감
O(n) 선형 시간이 소요된다.

데이터 추가

6과 2 사이에 21을 추가했을 때, 아래와 같이 진행된다
6의 포인터 영역은 새롭게 만든 21을 가리키고, 21은 2를 가리키게 된다
O(1) 상수 시간만 소요된다

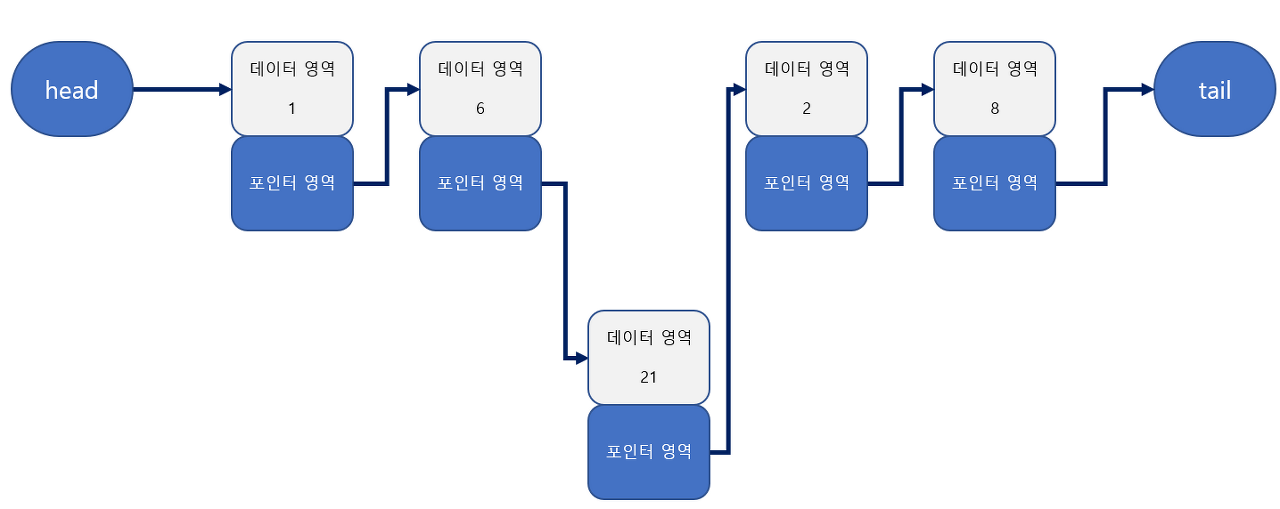
데이터 삭제

2를 삭제했을 때, 아래 사진과 같이 진행된다
21의 포인터 영역을 2의 포인터 영역인 8로 이어준 후, 2를 삭제한다
O(1) 상수 시간만 소요된다

Singly Linked List 코드 (예외처리 + 'size' 메소드 추가)

class Node {
  constructor(value) {
    this.value = value;
    this.next = null;
  }
}

class SinglyLinkedList {
  constructor() {
    this.head = null;
    this.tail = null;
    this.size = 0;
  }

  find(value) {
    let currentNode = this.head;
    
    while (currentNode !== null && currentNode.value != value) {
      currentNode = currentNode.next;
    }
    
    if (currentNode === null) {
      console.log(`FindError...Can't find the value : ${value}`);
    }
    return currentNode;
  }
  
  append(value) {
    const newNode = new Node(value);
    
    if (this.head === null) {
      this.head = newNode;
      this.tail = newNode;
    } else {
      this.tail.next = newNode;
      this.tail = newNode;
    }
    this.size++;
  }

  insert(node, value) {
    if (node === null) {
      return;
    }
    
    const newNode = new Node(value);
    newNode.next = node.next;
    node.next = newNode;
    this.size++;
  }

  remove(value) {
    let prevNode = this.head;
    
    while (prevNode.next.value !== value) {
      prevNode = prevNode.next;
    }
    
    if (prevNode.next !== null) {
      prevNode.next = prevNode.next.next;
      this.size--;
    } else {
      console.log(`RemoveError...Can't find the value : ${value}`);
    }
  }

  display() {
    let currentNode = this.head;
    let displayString = "[";

    while (currentNode !== null) {
      displayString += `${currentNode.value}, `;
      currentNode = currentNode.next;
    }

    displayString = displayString.substr(0, displayString.length - 2);
    displayString += "]";
    console.log(displayString);
  }

  getSize() {
    console.log(this.size);
  }
}

const linkedList = new SinglyLinkedList();
linkedList.append(1);
linkedList.append(2);
linkedList.append(4);
linkedList.append(7);
linkedList.display();
linkedList.insert(linkedList.find(4), 21);
linkedList.display();
linkedList.remove(2);
linkedList.display();

Doubly Linked List (이중 연결 리스트)

양방향으로 이어지는 연결 리스트
Singly Linked List보다 자료구조의 크기가 조금 더 크다 (이전 노드를 카르키는 메모리가 있어야 하기 때문)

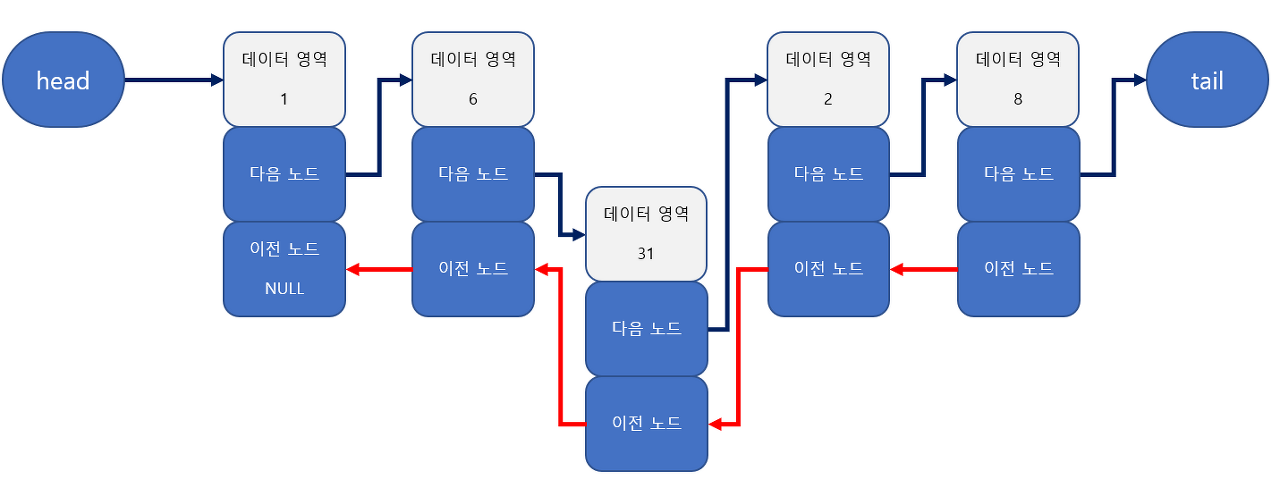
데이터 추가

31을 6과 2 사이에 추가해보기

우선 새롭게 만든 31의 다음 노드를 6의 다음 노드인 2로 연결한다
2의 이전 노드는 31을 가리키도록 한다
6의 다음 노드를 31로 연결한다
31의 이전 노드를 6으로 연결한다

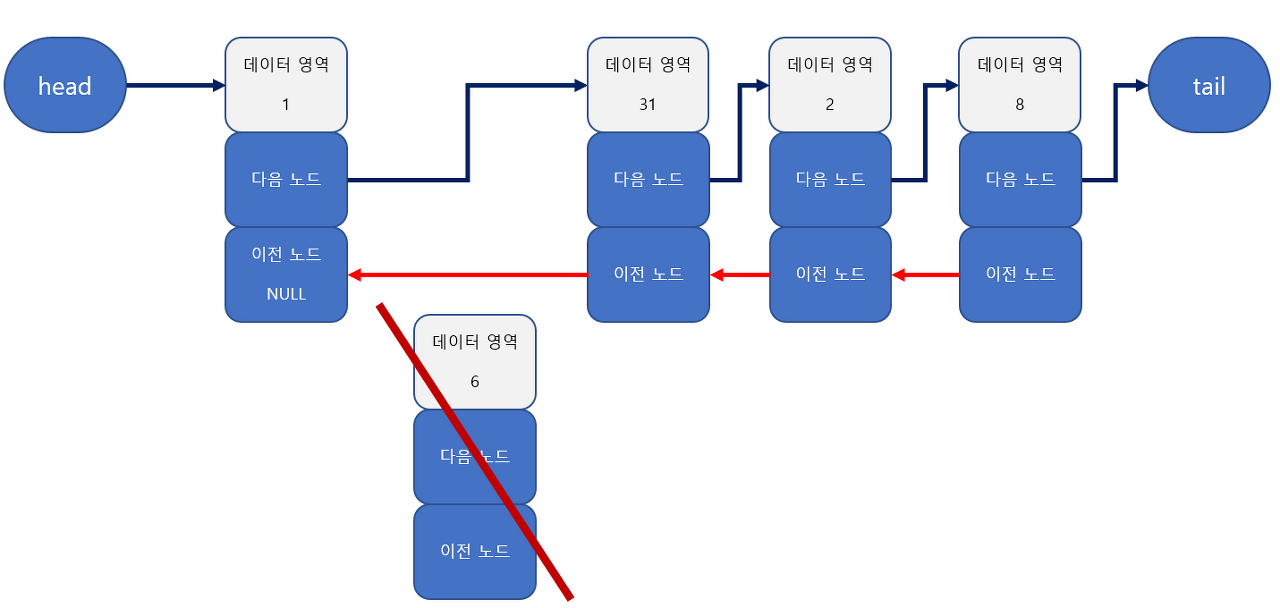
데이터 삭제

6을 지웠을 경우다

31의 이전 노드를 6의 이전 노드인 1을 가리키도록 한다
1의 다음 노드를 31로 바꾼다
6을 삭제한다

Doubly Linked List 코드

class Node {
  constructor(value) {
    this.value = value;
    this.prev = null;
    this.next = null;
  }
}

class DoublyLinkedList {
  constructor() {
    this.head = null;
    this.tail = null;
    this.size = 0;
  }

  find(value) {
    let currentNode = this.head;

    while (currentNode !== null && currentNode.value != value) {
      currentNode = currentNode.next;
    }

    if (currentNode === null) {
      console.log(`FindError...Can't find the value : ${value}`);
    }

    return currentNode;
  }

  append(value) {
    const newNode = new Node(value);

    if (this.head === null) {
      this.head = newNode;
      this.tail = newNode;
    } else {
      this.tail.next = newNode;
      this.tail = newNode;
      newNode.prev = this.tail;
    }
    this.size++;
  }

  insert(node, value) {
    if (node === null) {
      return;
    }

    const newNode = new Node(value);

    node.next.prev = newNode;
    newNode.prev = node;
    newNode.next = node.next;
    node.next = newNode;
    this.size++;
  }

  remove(value) {
    let prevNode = this.head;

    while (prevNode.next !== null && prevNode.next.value !== value) {
      prevNode = prevNode.next;
    }

    if (prevNode.next !== null) {
      prevNode.next = prevNode.next.next;
      this.size--;
    } else {
      console.log(`RmoveError...Can't find the value : ${value}`);
    }
  }

  display() {
    let currentNode = this.head;
    let displayString = "[";

    while (currentNode !== null) {
      displayString += `${currentNode.value}, `;
      currentNode = currentNode.next;
    }

    displayString = displayString.substr(0, displayString.length - 2);
    displayString += "]";
    console.log(displayString);
  }

  getSize() {
    console.log(this.size);
  }
}

const dll = new DoublyLinkedList();
dll.append(1);
dll.append(6);
dll.append(2);
dll.append(8);
dll.display();
dll.insert(dll.find(6), 31);
dll.display();
dll.remove(6);
dll.display();

Circular Linked List (환형 연결 리스트)

Singly 혹은 Doubly Linked List에서 Tail이 Head로 연결되는 연결 리스트
메모리를 아껴쓸 수 있다
원형 큐 등을 만들 때도 사용된다

Circular Linked List 코드

스택

Last In First Out이라는 개념을 가진 선형 자료구조
바닥이 막힌 상자를 생각하면 편함